Eksamensforelesning TDT4120

Algoritmer og Datastrukturer

Håvard Krogstie - høsten 2021

Raskt tilbakeblikk på Store O

Aldri for gammel for enda mer Store O

$\begin{array}{ccc} a < b & \Leftrightarrow & b > a \\ \Downarrow & & \Downarrow \\ a \leq b & \Leftrightarrow & b \geq a \\ \Uparrow & & \Uparrow \\ a = b & \Leftrightarrow & b = a \end{array}$

$\begin{array}{ccc} a = \mathrm{o}(b) & \Leftrightarrow & b = \mathrm{\omega}(a) \\ \Downarrow & & \Downarrow \\ a =\mathrm{O}(b) & \Leftrightarrow & b = \mathrm{\Omega}(a) \\ \Uparrow & & \Uparrow \\ a = \mathrm{\Theta}(b) & \Leftrightarrow & b = \mathrm{\Theta}(a) \end{array}$

Eksamensforelesning TDT4120

Algoritmer og Datastrukturer

Håvard Krogstie - høsten 2021

Raskt tilbakeblikk på Store O

Aldri for gammel for enda mer Store O

$\begin{array}{ccc} a < b & \Leftrightarrow & b > a \\ \Downarrow & & \Downarrow \\ a \leq b & \Leftrightarrow & b \geq a \\ \Uparrow & & \Uparrow \\ a = b & \Leftrightarrow & b = a \end{array}$

Husk at det er asymptotisk (u)likhet

Og at disse greske bokstavene egentlig er mengder

$\mathrm{\Theta}(n^2) = \left\{4n^2 + 3n,\ \ \ \frac{1}{2}n^2 + 67n\log{n},\ \ \ n^2-45n+6\right\}$

$f(n) = \mathrm{\Theta}(g(n))\ \ \ \ \Rightarrow\ \ \ \lim_{n\rightarrow\infty} \frac{f(n)}{g(n)} = C,\ \ \ 0 < C < \infty$

Ta store O på tavla

Ekstrem misbruk av likhetstegn

Men la gå

$f(n) = \mathrm{O}(g(n))$

Betyr egentlig

$f(n) = X,\ \ \ \ \ \ \text{ der }\exists X\in\mathrm{O}(g(n))$

$\mathrm{O}(n^2) + \mathrm{O}(n^3) = \mathrm{O}(g(n))$

Betyr egentlig

$\forall X \in \mathrm{O}(n^2),\\ \forall Y \in \mathrm{O}(n^3),\\ \exists Z \in \mathrm{O}(g(n))\\ \text{slik at} \\ X + Y = Z$

Oppgave

Fra en av Øvingene, men likevel relevant, skulle jeg mene

Eksamensoppgave

Desember 2017

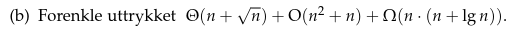
Heaps og binære søketrær

Temmelig like, men også ulike

Binære søketrær

INORDER-TREE-WALK
TREE-SEARCH
TREE-MINIMUM
TREE-MAXIMUM
TREE-SUCCESSOR
TREE-PREDECESSOR
TREE-INSERT

Balansering og høyde

Heaps

PARENT
LEFT
RIGHT
MAX-HEAPIFY
BUILD-MAX-HEAP
HEAPSORT
MAX-HEAP-INSERT
HEAP-EXTRACT-MAX
HEAP-INCREASE-KEY

Lagres kompakt!

Oppgave

Eksamen august 2019

Oppgave

Eksamen November 2019

Bruke heap som prioritetskø

En liten oppgave

Du er gitt en liste med $n$ tall.
Du ønker å fjerne tall fra listen, slik at ingen prefikser til listen har negativ sum.
Fjern så få tall som mulig.

Dynamisk programmering

Eksamen November 2020

Stavkutting

To hovedmåter å implementere DP

Memoisering (top-down)
Iterasjon (bottom-up)

Begreper

optimale løsninger
optimal delstruktur
overlappende delinstanser

Eksamensoppgave

November 2019

Krabbedans

Jeg tar med noe hjemmesnekk

Hvorfor tar jeg med denne

Knapsack og LCS er vanskelig å visualisere.
Å lage "noder" av tidsaksen er et vanlig knep.

Kjekt å vite

I AlgDat kalles ofte forgjenger-matrisen $\pi$ .

Grådige algoritmer

Da slipper vi DP!

I sted trengte vi DP, siden vi måtte prøve alle delinstanser.

Hva om vi bare tar den som ser mest lovende ut?

Hvis det er globalt optimalt å gjøre det som er lokalt optimalt, oppfylles grådighetsegenskapen.

Huffmann-enkoding

Grådighet funker

Oppgave

Eksamen desember 2018

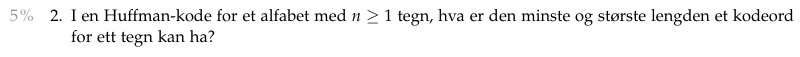
Annen grådig-oppgave

Eksamen august 2019

Grafer

Viktige begreper å kunne

Node
Kant
Rettede kanter
Vektede kanter
Enkel graf (simple graph)

Representasjoner:

Naboliste
Nabomatrise

Traversering av grafer: BFS

Den som bruker en kø

Med BFS = bredde-først-søk finner vi korteste vei fra én node til alle andre.
Fungerer bare hvis kantene ikke har vekter.
Kantene kan ha retning, det går fint.

Bruker en kø.
Holder oversikt over besøkte noder.
Begynner med kun start-noden i køen.

$\mathrm{O}(|V| + |E|)$

Traversering av grafer: DFS

Den som bruker en stakk

Med DFS = dybde-først-søk lager vi en slags ordning.

Bruker en stakk.
Har også en "tid-teller". Holder oversikt over besøk-start og besøk-slutt for hver node.
Kan trenge flere start-noder.

$\mathrm{O}(|V| + |E|)$

DFS sin kant-klassifisering

Vi ender opp med et tre, pluss eventuelle ekstra noder

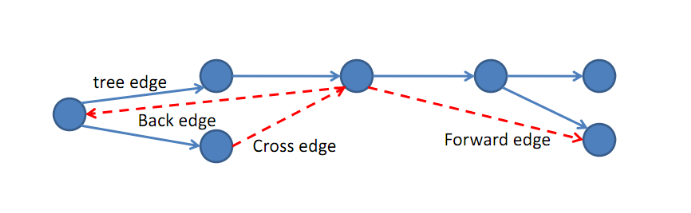
Parantesteoremet og hvit-sti-teoremet

Angår altså DFS

Én node sin start- og slutt-tid vil aldri delvis overlappe med en annens.

Hvis $u$ er etterkommer av $v$ , var det kun hvite noder fra $v$ til $u$ da $v$ ble grå.

Toplogisk sortering

Vi bruker de derre slutt-tidene etter å ha gjort DFS

Sorter alle nodene etter slutt-tid. Størst først.
For alle noder $u$ der det finnes en vei til $v$ , vil $u$ kommer før $v$ .

Fungerer ikke hvis grafen har back-edge. Da har den sykler.

Tenketid

En liten oppgave

Vi har $n$ forfattere, og $k$ artikler.
Hver artikkel er skrevet av enten $1, 2, 3, \ldots n$ forfattere.

Hvis forfatter $A$ og forfatter $B$ begge to har skrevet på samme artikkel, er de medforfattere.

Forfatter nummer $1$ er Erdős. Han har Erdős-tall $0$ .
Alle som er medforfatter med Erdős har Erdős-tall $1$ .
Medforfatterne deres igjen, har Erdős-tall $2$ .

Erdős-tall er altså antall "hopp" mellom medforfattere som må gjøres for å nå Erdős.
Finn alle forfatternes Erdős-tall.

Minimale spenntrær

Alle noder skal med, men billigst mulig kanter, takk

Vi har en vektet urettet graf.

Spenntrær kobler sammen alle nodene, uten å lage sykler.

Minimale spenntrær velger de billigste kantene.

Her fungerer det å være grådig.

Kruskal

Én måte å finne minimale spenntrær

Sorter alle kantene etter vekt. Minst først.
Legg til én og én av kantene, med mindre det skaper en sykel.

Raskt sjekke om to noder er koblet fra før?
Disjoint set data structure (union find).

Prims

Enda en måte å finne minimale spenntrær

Begynn med én node. Dette blir roten.
Ha en prioritetskø over alle kanter som stikker ut av treet ditt.

Korteste vei én til alle

I en vektet, muligens rettet graf

Obs! Negative sykler er et problem!

Kan vi løse negative sykler ved å kun godta enkle veier?

BELLMAN-FORD oppdager hvertfall negative sykler. DJIKSTRA blir grundig lurt og vil holde på til evig tid.

Dette har også betydning for spørsmålet lengste vei.

Bellman-ford

Relax relax relax

Begynn med at alle noder er $\infty$ langt unna start.
For hver kant, prøv å slakke! RELAX!

Etter å ha slakket alle kanter, $|V|-1$ ganger, vil alle stier være funnet!

Vi kan kanskje slutte tidligere! Eller negativ sykel!

$\mathrm{O}(|E||V|)$

Dijkstra

Den klassiske korteste vei fra én til alle

Gi gjør det samme som PRIM, men med total avstand fra start.

\mathrm{O}(|V|\lo)

Oppgave

Eksamen aug 2019

Floyd-Warshall

Korteste vei, alle til alle

Lag en matrise med korteste kjente avstand mellom alle par.

$\mathrm{O}(|V|^3)$

Maksimal flyt

La ditt rike flomme

Vi har en graf med en kran og et sluk,
der hver kant har en retning og kapasitet.

Har vi en urettet graf, doble alle kanter!

Vi vil sende vann gjennom rørene, slik at mest mulig vann flyter gjennom.

FORD-FULKERSON-METHOD beskriver augmenting paths

EDMONDS-KARP beskriver hvordan vi finner augmenting paths med BFS.

Minimalt snitt

Faktisk akkurat samme problem, en såkalt dual

Vi velger de kantene som er helt fulle.
Snipp snipp.

NP-kompletthet

Noen ting er rett og slett vanskelige

Vi ser på ja-nei-problemer (beslutnings-problemer).
"Finnes det en enkel vei som besøker alle noder?"

Klassen NP er problemer der ja-svar kan verifiseres i polynomisk tid.

Alt i NP kan reduseres til de NP-komplette problemene.
De er de vanskeligste problemene vi har i NP.

Alt som er NP-komplett eller vanskeligere er NP-hardt.

co-NP

Nesten det samme

Klassen vo-NP er problemer der nei-svar kan verifiseres i polynomisk tid.

Oppgave

Eksamen august 2019